C Language Implementation for Proportional-Resonant Controller
1. Introduction to Proportional-Resonant Controller
First, let’s see the transfer function of PR controller and its bode diagram:
$$ G_{PR}(s)=K_{p} + \frac{K_{r}s}{s^{2} + \omega_{r}^2} $$
where the $\omega_{r}$ is the resonant frequency.
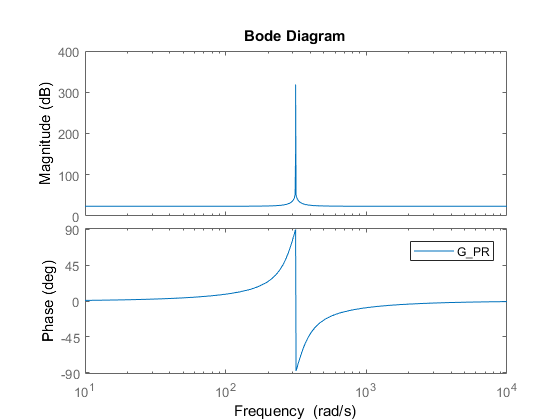
As can be seen in the bode diagram, the gain at 50Hz (314 rad/s) is infinite, so PR controller can be used to track reference of specific frequency. However, the reference frequency is not always a constant, e.g. the frequency of electricity grid. In practice, Quasi-Proportional-Resonant(QPR) can be used to solve this problem.
The transfer function of QPR and its bode diagram:
$$ G_{QPR}(s) = K_{p} +\frac{2 \omega_{i} Kr s}{s^{2} + 2\omega_{i}s + \omega_{r}^{2}} $$
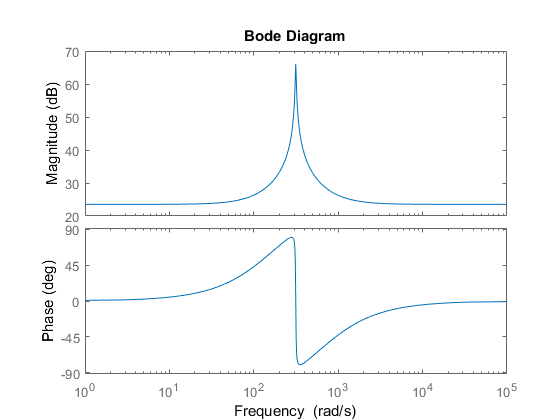
where the addition of $2 \omega _{i}$ reduces the gain at resonant frequency but increase the band width around resonant frequency.
You can change the parameter $\omega_{r}$ and run the demo code below to see how it changes the shape of bode diagram.
s = tf([1, 0], 1) ;
Kp = 15 ;
Kr = 2000 ;
wr = 50 * 2 * pi ;
wi = pi ;
G_PR = Kp + Kr * s / (s^2 + wr^2)
figure
bode(G_PR)
G_QPR = Kp + 2 * wi * Kr * s / (s^2 + 2 * wi * s + wr^2)
figure
bode(G_QPR)
2. Implementation in C
The code is in the repository Controller, feel free to use it for your own application.
The structure of QPR controller implemented is as below:
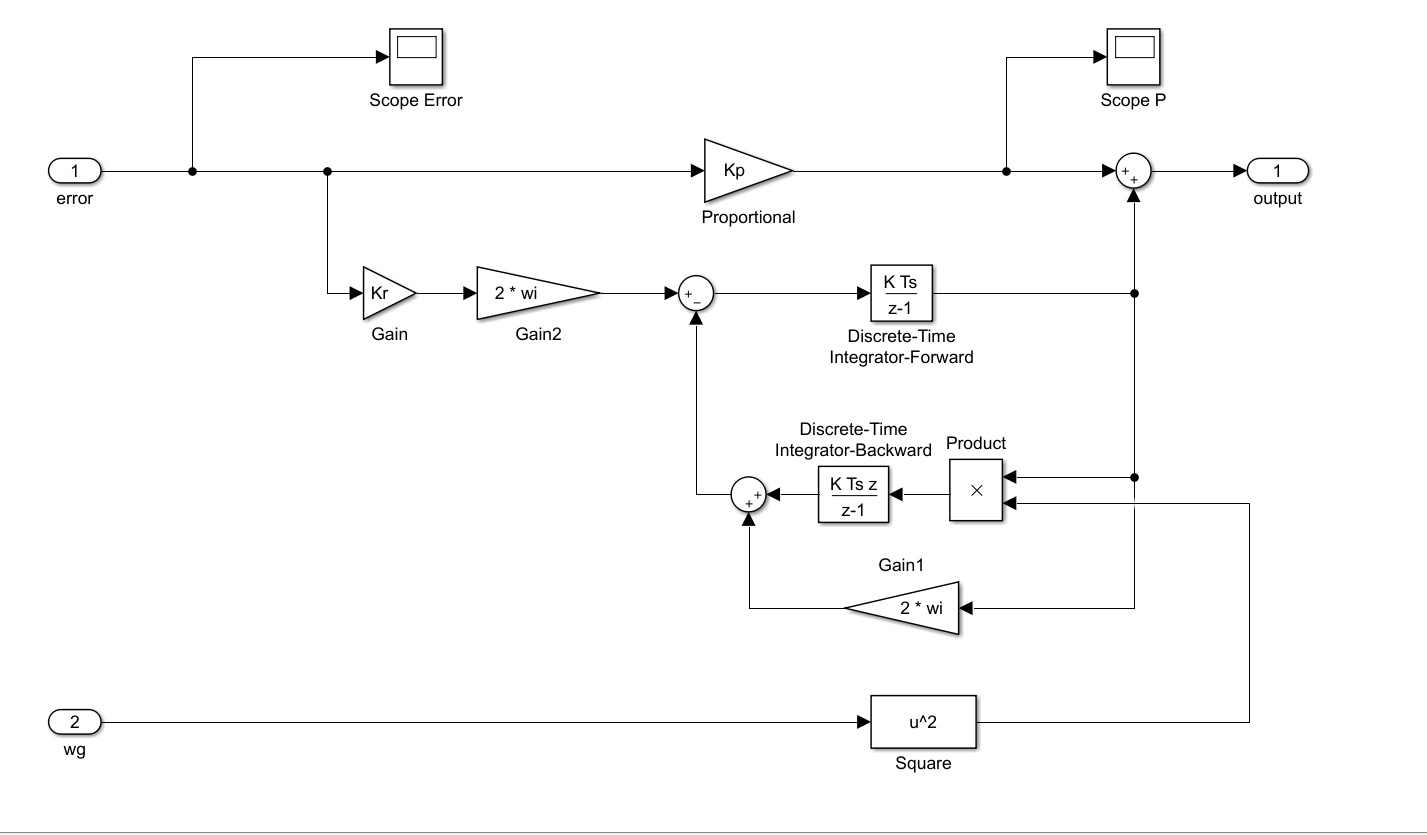
As shown in this paper, the structure of QPR controller can be implemented using 2 integrators.
The implemented structure above has 2 advantages:
- Easy to implemented, only 2 integrators used.
- Autonomous resonant frequency adaption: $\omega_{r}$ can be fed into the controller and real-time resonant frequency adaption is achieved.
You can run this demo to see the effectiveness of this structure
- $K_{p}$ is set to be 0 and $K_{r}$ to be 10
- $\omega_{i}$ is set to be $0.01 \omega_{r}$
The output response is as below:
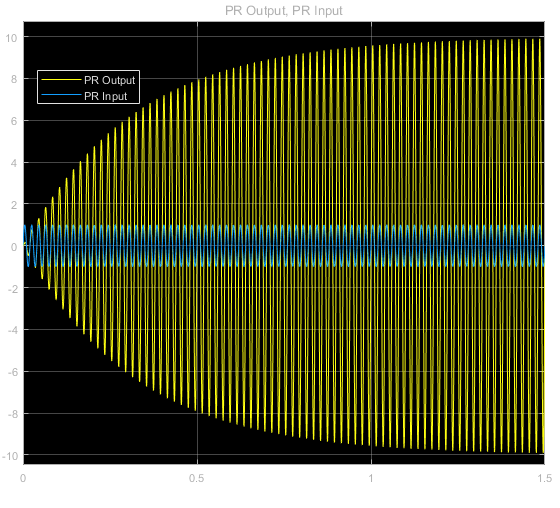
As you can see in the result above, the input signal is a sine wave with an amplitude of 1 and the output with an amplitude of 10, corresponding to the parameter– $K_p$ is 0 and $K_r$ is 10.